 |
||||||||
Organizational Effectiveness Through Feedback Management
|
||||||||
|
>> Statistical Confidence in a Survey:
|
||||||||
Dr. Fred Van Bennekom
conducted a webinar
in conjunction with GainSight
on March 30, 2013 on the
Hidden Dangers
of Survey Bias
|
||
Review our
Read our latest article on
and its shortcomings
|
||
|
||
|
||
Learn how to conduct a survey project from questionnaire design
to survey administration
to data analysis.
 June 11-13, Denver COJuly 2-4, Dubai UAESept. 24-26, Washington DCOct. 19-20, Nashville (Survey Design only.)~~~
Recorded Webinar Avallable On DemandLive Offering Summer 2013~~~
Offering TBD
~~~
Learn how to design a
Offering TBD
~~~
View a short online presentation
summarizing the concept of surveying and outlining our courses.
|
||
Private On-site
Survey Workshops
are available at your company. This may prove more cost effective and deliver immediate value to your survey program as we build your survey instrument in class.
Please contact us for details.
|
||
Provides targeted assistance on your survey questionnaire and project while being mentored on good survey practices.
|
||
Need more than
targeted survey consulting?
Great Brook specializes in
the design and execution of
Custom Survey Research Projects to meet
your individual needs.
|
||
Get an expert's review of the feedback management processes in your organization for customers or other stakeholder groups --
or get a deep dive assessment of your survey program.
|
||
|
||
Have a question about surveying you'd like to have answered in a future newsletter article?
Please contact us.
|
||
Self-help guidance for your survey project
 |
||
For a comprehensive list
of survey automation tools
for your survey program.
|
How Many is Enough?
When I do conference presentations, I am inevitably asked about typical survey response rates -- usually before I get to that part of my presentation. Questions or statements range from:
“My marketing organization says if I get a 3% to 5% return, I should be happy. Is that right?”“What's the national average survey response rate?”"What's a good survey response rate?"“A colleague did a project and the consultant said they had a good statistical confidence with 25% response rate. He had 1000 customers he surveyed (and got 250 responses). I have about 200 customers. Can I just extrapolate down and apply that 25% to my situation?”I have also heard two conference presenters get asked about survey response requirements -- even though that wasn't the primary topic of the talks and far from their areas of expertise -- and say that 30 responses was all you need for valid results. (I think they recalled the Central Limit Theorem from a statistics class.)
I groaned...
If only life -- and statistics -- were so simple.
Everyone conducting a survey is concerned about response rates and the level of confidence they can place in the survey results. This is one part of a survey project that does require some fundamental understanding of statistics. In my Survey Design Workshop, I spend considerable time on this topic, and I can tell those people who had a college stats class -- and blissfully forgot everything upon walking out of the final exam room. These people tend to shake uncontrollably when I say “statistical inference.”
Follow this link for a free survey sample size calculator
in Excel that generated the nearby chart.
It can also be used to calculate statistical accuracy
based on the response group size
|
Here's an obvious statement: the more completed surveys you get, 1) the greater the confidence and 2) the greater the cost. So, a trade-off exists between two objectives in a survey project: maximize confidence but minimize costs. The extent of the trade-off depends upon the administration technique employed, but that's the topic for another article.
Four factors determine the statistical confidence:
Size of the population. The population is the group of interest for the survey. A sample is drawn from the population and the survey is administered to the sample. Some percentage of the sample responds to the survey invitation. That percentage is the response rate. Segmentation analysis desired. Typically, we analyze the data set as whole, but we also typically analyze the data along some demographic segmentation, for example, region, annual sales volume, or support representative. Each segment in essence is another population. If the critical business decisions will be focused on the analysis of a segment, then statistical confidence must be focused on the segment, not the population. Degree of variance in responses from the population. This factor is the hardest to understand for the statistically challenged. If the respondents' responses tend to be tightly clustered, then we don't need to sample as many people to get the same confidence as we would if the responses range widely. Imagine you polled your office colleagues, and the first five people gave the same answer. Would you continue polling? Probably not. What if you got five different responses? You'd probably keep polling. Therefore, more variability requires larger samples. But until we do some surveying and analyze the data, we don't know anything about the variance! So, initially, we need to employ conservative assumptions about the variance.
Tolerance for error. How accurate do you need the results to be? If you're going to make multi-million dollar business decisions, then you probably have less tolerance for error. But how many is enough? The statistical equations here are a bit daunting. (They can be found in most any statistics textbook under "sample size.") Each of the above four factors is reflected in the equations. To make it more understandable, look at the nearby survey response rate requirement chart, which can also be found as a PDF file by following that link.
The horizontal axis shows the population. The vertical axis show the percentage of the population from whom we have a response. This is not the response rate. The response rate is the percentage of those receiving an invitation who respond. Note the critical distinction.
The chart shows seven lines or curves that depict seven levels of accuracy. The first one is the horizontal line at the top. If we perform a census and everyone responds, then we are 100% certain that we are 100% accurate. We have population parameters. Of course, that will likely never happen.
Before I explain how to interpret the curves, let's bring out a couple of points from the chart. First, as the percentage responding increases, the accuracy increases. No surprise there. Second, as the size of the population grows, the percentage responding needed for the same level of accuracy decreases. Conversely, when we have a small population, we have to talk to a larger percentage of the population for reasonable accuracy. Please note: this chart employs the most conservative assumption about the variance of responses -- item 3 above.
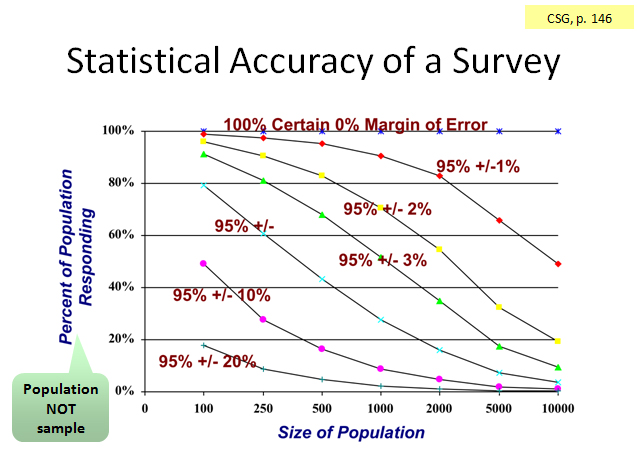
Now let's interpret those curves. Each curve shows 95% certainty of some range of accuracy. The 95% is chosen by convention. Let's focus on the accuracy part of the statement. Let's say we have an accuracy of +/- 10%, and our questions use an interval scale that ranges from 0 to 5 (so there are 5 equal intervals in the scale). Let's say we get sufficient responses so we're on the +/-10% curve. Plus or minus 10% on our scale is 1 full interval point (20% of 5).
If we conducted this survey 20 times, 19 out the 20 times (95%), we would expect the mean score to lie within +/-10% of the mean score found when we conducted the survey. Although, technically incorrect, it's sometimes easier to interpret it the following way. If we got responses from everyone in the population, we are 95% certain that average (the population mean) would lie within a band of 1 point on our scale with the average score from a survey question (the sample mean) in the middle.
Take a deep breath and re-read the above…
Say you have a population of 1000, and you sent a survey invitation to 500 people. Half of those responded. So, 25% of the population responded. Find the intersection of 1000 on the horizontal axis and 25% on the vertical axis. You would be approximately 95% certain of +/-5% accuracy in your survey results.
Conversely, if we have an accuracy goal for the survey project, we can use this chart to determine the number of responses needed. Say, we have that population of 500, and we wanted an accuracy of +/-10%. Then we would need about 18% of the population to respond, or 90. (Find those coordinates on the chart.) By applying an estimate of our response rate, we can then determine the number of survey invitations we must send out, which is our sample size. If we estimated a 25% response rate, then we would need a sample size of 360. (360 x .25 = 90)
Take another deep breath and re-read the above…
When we actually conduct our survey and analyze the results, we will then know something about the variance in the responses. The confidence statistic incorporates the variance found in each survey question and can be calculated for each survey question. The confidence statistic tells us the size of the band or interval in which the population mean most likely lies - with a 95% certainty. (Technically, the interval tells us where the mean of repeated survey samples would fall. With a 95% certainty, 19 of 20 survey samples drawn from the population of interest would lie within the confidence interval.)
Look at the second chart in the linked file. That shows the calculation of the confidence statistic using Excel. Alpha is likelihood of being wrong we're willing to accept. (.05 or 5% being wrong is the same as 95% certainty we're correct.) The standard deviation is square root of the variance, and can be calculated using Excel. Size is the number of responses. In this example, the mean for the survey question was 3.5 on a 1 to 5 scale (not a 0 to 5 scale!) and the confidence was 0.15. So, we're 95% certain the true mean or population mean lies in a band defined by 3.5 +/-0.15. Our accuracy is 0.15 as a percentage of the size of the scale, which is 5-1=4. Thus, our accuracy is +/-3.75%.
Let's close by dispelling the myths in the opening three quotes.
The response to a direct mail campaign is completely and utterly irrelevant to the statistical accuracy of a survey. In other words, beware of whose advice you take! (Some of the worst advice you will get about surveys will come from people who claim to be market researchers.)There is no national average response rate. It will be affected by a whole host of factors, which I'll address in a future article. Response rates and statistical confidence are not linear.Finally, 30 responses would provide acceptable accuracy only if a) you have a very small population, b) you have very little variance in the responses, or c) you are willing to accept very low accuracy. As a very rough rule of thumb, 200 responses will provide fairly good survey accuracy under most assumptions and parameters of a survey project -- except for analysis within each segment! 100 responses are probably needed even for marginally acceptable accuracy.You don't need to be a statistician to do a survey, but you should ask those questions about the statistical confidence of your results. Again, if you'd like the response rate calculator in Excel that generated the chart, please contact us.
-- Fred Van Bennekom, Dr.B.A., Principal Great Brook Consulting
Please contact us with feedback on this article or other topics that you might find interesting.